8和10的最大公因数是多少

8=2*4,10=2*5,即8和10的最大公因数是2。最大公因数,也称最大公约数、最大公因子,指两个或多个整数共有约数中最大的一个。a,b的最大公约数记为(a,b),同样的,a,b,c的最大公约数记为(a,b,c),多个整数的最大公约数也有同样的记号。求最大公约数有多种方法,常见的有质因数分解法、短除法、辗转相除法、更相减损法。与最大公约数相对应的概念是最小公倍数,a,b的最小公倍数记为[a,b]。
8和9的最大公因数和最小公倍数是什么
8=2×4,1O=2×5
最大公因数是2
5×8=40
4×10=40
最小公倍数是40
5和9最大的公因数是什么
8和10最大的公因数是(2)。
用短除法表示如下:
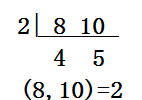
短除法
100和8的最大公因数
10和8的最大公因数:2。
公因数,亦称“公约数”。它是一个能同时整除若干整数的整数。如果一个整数同时是几个整数的因数,称这个整数为它们的“公因数”;公因数中最大的称为最大公因数。对任意的若干个正整数,1总是它们的公因数。
给定若干个整数,如果有一个数是它们共同的因数,那么这个数就叫做它们的公因数。而全部公因数中最大的那个,称为这些整数的最大公因数。公约数与公倍数相反,就是既是A的约数同时也是B的约数的数。

公因数,又称公约数。在数论的叙述中,如果n和d都是整数,而且存在某个整数c,使得n=cd,就说d是n的一个因数,或说n是d的一个倍数,记作d|n(读作d整除n)。如果d|a且d|b,我们就称d是a和b的一个公因数。
根据裴蜀定理,对每一对整数a,b,都有一个公因数d,使得d=ax+by,其中x和y是某些整数,并且a和b的每一个公因数都能整除这个d。于是d的绝对值叫做最大公因数。求几个整数的最大公因数,只要把它们的所有共有的质因数连乘,所得的积就是它们的最大公因数。

短除法:
短除法:短除法求最大公约数,先用这几个数的公约数连续去除,一直除到所有的商互质为止,然后把所有的除数连乘起来,所得的积就是这几个数的最大公约数。短除法的本质就是质因数分解法,只是将质因数分解用短除符号来进行。
短除符号就是除号倒过来。短除就是在除法中写除数的地方写两个数共有的质因数,然后落下两个数被公有质因数整除的商,之后再除,以此类推,直到结果互质为止(两个数互质)。
8和9的最大公因数和最小公倍数
10和8的最大公因数是2,最小公倍数是40。

最大公因数就是一个数或两个数的共同因数,并且是最大的。
最小公倍数就是一个数或两个数的共同倍数,并且是最小的。
公因数是能同时整除若干整数的整数。如果一个整数同时是几个整数的因数,称这个整数为它们的公因数,公因数中最大的称为最大公因数。
公倍数是指在两个或两个以上的自然数中,如果它们有相同的倍数,这些倍数就是它们的公倍数。公倍数中最小的,就称为这些整数的最小公倍数。

常用结论
在解有关最大公约数、最小公倍数的问题时,常用到以下结论:
(1)如果两个自然数是互质数,那么它们的最大公约数是1,最小公倍数是这两个数的乘积。
例如8和9,它们是互质数,所以(8,9)=1,[8,9]=72。
(2)如果两个自然数中,较大数是较小数的倍数,那么较小数就是这两个数的最大公约数,较大数就是这两个数的最小公倍数。
例如18与3,18÷3=6,所以(18,3)=3,[18,3]=18。
(3)两个整数分别除以它们的最大公约数,所得的商是互质数。
例如8和14分别除以它们的最大公约数2,所得的商分别为4和7,那么4和7是互质数。
(4)两个自然数的最大公约数与它们的最小公倍数的乘积等于这两个数的乘积。
例如12和16,(12,16)=4,[12,16]=48,有4×48=12×16,即(12,16)× =12×16。
以上就是关于8和0的最大公因数是多少的全部内容,以及8和10的最大公因数是多少的相关内容,希望能够帮到您。
